费马点模型
一、费马点的由来
费马,17世纪法国数学家,有“业余数学家之王”的美誉,之所以叫业余并非段位不够,而是因为其主职是律师,数学只是兼职搞搞。
费马在解析几何、微积分等领域都有卓越的贡献,除此之外,费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等.
据说费马在提出“费马大定理”时,是他在给另一位数学家欧拉的信中提出来的,他写道:“我已经想到了一个绝妙的证明方法,但是这个地方不够写,我就不写了吧”
结果这个问题困扰了数学界300多年,直到1995年,才由英国数学家怀尔斯证明出,而距离费马逝世,已经过去了330年。
果然,数学搞得好的都是装x的一把好手。
在书信中提问题,似乎是费马通信的一贯作风,在一封写给意大利物理学家兼数学家托里拆利的信件中,费马提出了关于三角形的一个有趣问题:在三角形所在平面上求一点,使该点到三角形三个顶点距离之和最小.
请求托里拆利帮忙解答(其实费马自己已经证明了,就是想为难一下托里拆利)这当然难不倒另外一个业余数学家,托里拆利成功地解决了费马的问题。
所以说,今天的费马点问题不是费马解决的,而是他提出来,故而叫费马点,也叫托里拆利点。
二、中考“费马点”
费马点在最新教材中已不再提及,数学老师通常在课堂上作为拓展知识来讲解,但正是由于是拓展知识,很多学生不会太重视,甚至当初耳边风。
10年前的中考题里,考察这一知识点的情况比较常见。近年来,为了给学生减负,费马点问题不再作为考试大纲的考点。但是,有时候还是会以探索类的题型出现,就是换着花样来考。因此,为了在残酷的竞争中取得优势,我们仍然要把它作为一个重要的知识点加以掌握。
三、费马点的两种情况
1、如果三角形的三个内角均小于120度,费马点是对各边的张角都是120度的点。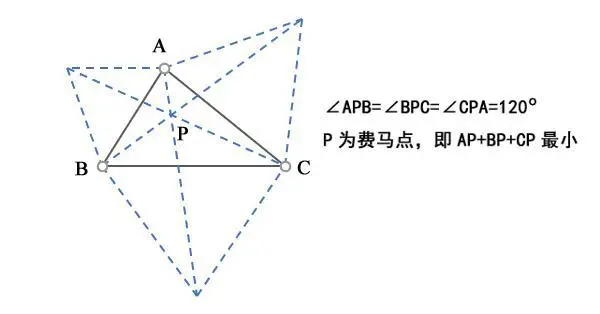
可以看出,费马点P就是以三角形三边为边长向外做的3个等边三角形的外顶点和ABC三点连线的交点。
2、如果有一个角大于或等于120度的三角形,费马点就是这个钝角的顶点。
四、费马点的证明
P为△ABC内任一点,请找点P使它到△ABC三个顶点的距离之和PA+PB+PC最小?
1、三个内角均小于120°的情形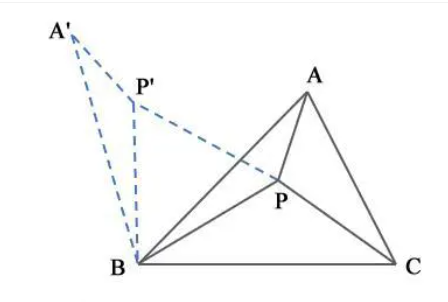
证明:如图,把△ABP绕B点逆时针旋转60°得到$$A′BP′,连接PP′,
则:△BPA≌△BP′A′
∴ PB=P′B,PA=P′A′,△BP′P为等边三角形,PB=PP′
∴ PA+PB+PC=P′A′+PP′+PC
∴ 当C、P、P′、A′四点共线时,PA+PB+PC为最小值
当C、P、P′共线时
∵ ∠BPP′=60°
∴ ∠BPC=120°
同理:当P、P′、A′共线时
∵ ∠BP′P=60°
∴ ∠A′P′B=120°
∴ ∠BPA=120°
∴ P点为满足∠BPC=∠BPA=∠APC=120°的点,即为费马点。
2、有一个内角均大于或等于120°的情形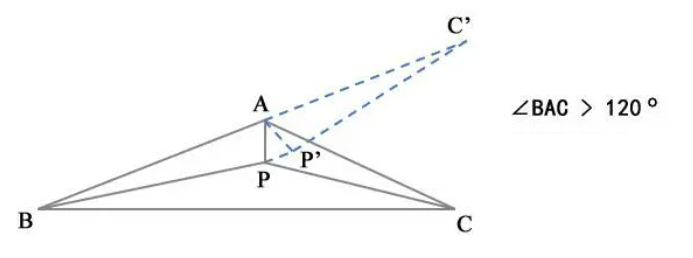
证明:如图,把△APC旋转到△AP′C′,使得B、A、C′三点在同一条直线上
∴ △APC≌△AP′C′,AP=AP′
∵ ∠BAC≥120°
∴ ∠PAP′=180°-∠BAP-C′AP′=180°-∠BAP-∠CAP=180°-∠BAC≤60°
∴ AP≥PP′
∴ PA+PB+PC≥PP′+PB+PC′>BC′=AB+AC
∴ A点为费马点
可以看出两种情况下的费马点证明都是依据旋转思想,构造三角形全等,然后将三条线段之和转化到是否在一条直线上来决定最小值。
例1、如图,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC内部的任意一点,连接PA,PB,PC,求PA+PB+PC的最小值.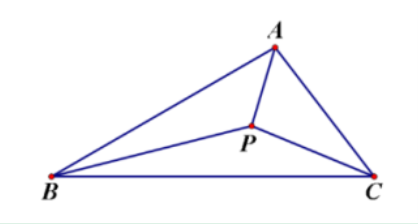
解:如图,将△ABP绕B点逆时针旋转60°,得到△DBE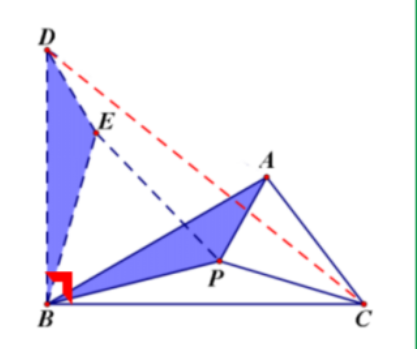
∴ △ABP≌△DBE,连接EP
∴ ∠ABP=∠DBE,BD=AB=4
∵ ∠PBE=∠ABD=60°,BE=PE,AP=DE,
∴ △BPE是等边三角形
∴ EP=BP
∴ PA+PB+PC=DE+EP+PC≥CD
∴ 当D、E、P、C四点共线时,PA+PB+PC有最小值CD
∵ ∠ABC=30°
∴ ∠DBC=∠ABD+∠ABC=90°
∴ CD=\sqrt{BD^2+BC^2}=\sqrt{41}
例2、如图,等腰Rt△ABC,直角边AB=4,点P为△ABC内部一点,求AP+BP+CP的最小值。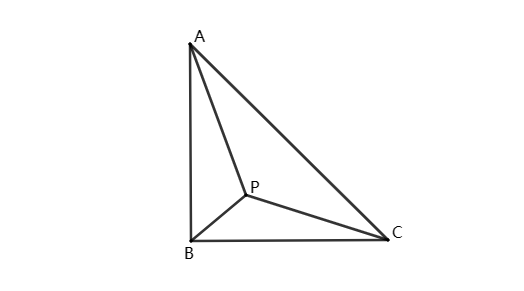
解:如图,将△ABP绕B点逆时针旋转60°,得到△A′BP′,连接PP′,A′C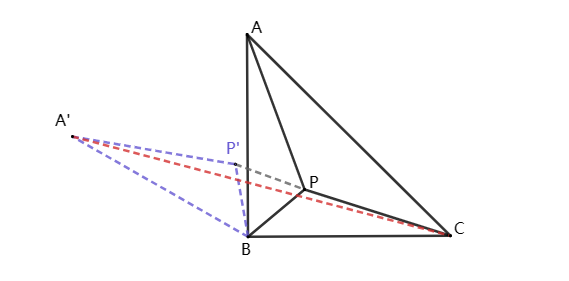
∴ △ABP≌△A′BP′,AP=A′P′,BP=BP′,∠PBP′=60°
∴ △BPP′为等边三角形
∴ PA+PB+PC=P′A′+P′P+PC≥A′C
∴ 当A′、P′、P、C四点共线时,PA+PB+PC的值最小
过A′作A′D⊥CB延长线于点D,如图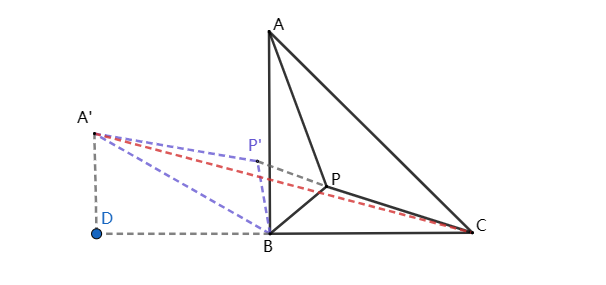
∵ ∠ABC=90°,∠P′BP=60°
∴ ∠DBA′=30°
∵ A′B=AB=4
∴ A′D=2
∴ DB=\sqrt{A′B^2-A′D^2}=\sqrt{4^2-2^2}=2\sqrt{3}
∴ DC=DB+BC=2\sqrt{3}+4
∴ A′C=\sqrt{A′D^2+DC^2}=\sqrt{2^2+(2\sqrt{3}+4)^2}=2\sqrt{2}+2\sqrt{6}
练习1、如图,在Rt△ABC中,AB=4, AC=8, 点P是△ABC内一点,求PA+PB+PC的最小值.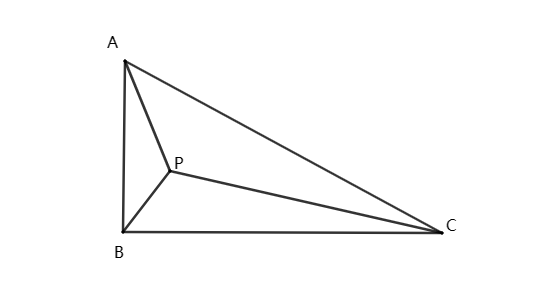
练习2、如图,已知,在△ABC中,∠ACB=30°,当AC=4,AB=\sqrt{7}(CB>CA),点P是△ABC内一点,求PA+PB+PC的最小值.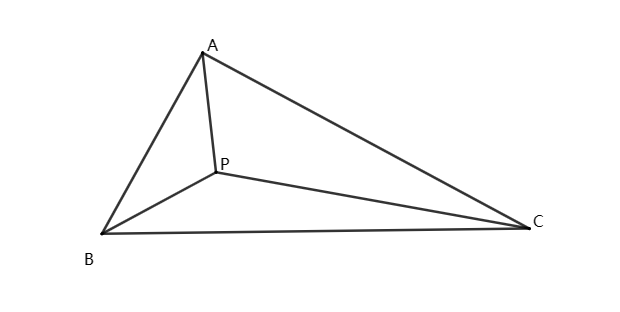
练习3、如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=\sqrt{3},点O为△ABC内一点,连接AO,BO,CO,若∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.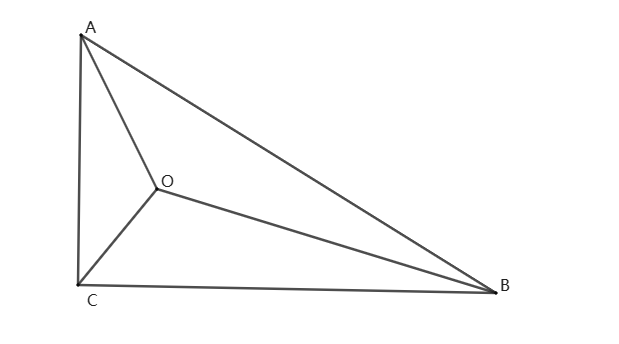
练习4、如图,菱形ABCD中,∠ABC=60°,在菱形ABCD内部有一点P.
① 请在图中画出是PA+PB+PC最小的线段(保留画图痕迹,画出一条即可)
② 若菱形的边长为4,请直接写出当PA+PB+PC值最小时PB的长.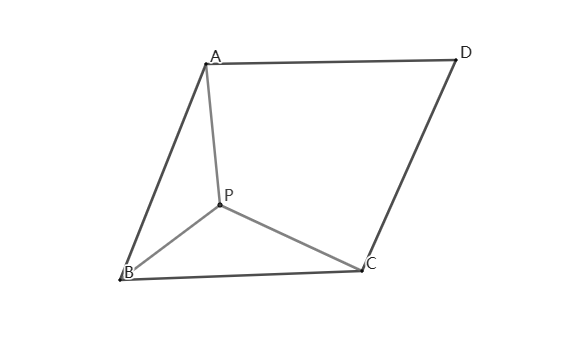
练习5、已知三村庄A、B、C构成如图所示△ABC(其中∠A、∠B、∠C均小于120°),现选取一点P打水井,使从水井P到三村庄A、B、C所铺设的输水管道长度最小,求输水管总长度的最小值.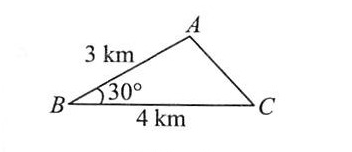
练习6、问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,可推出结论:PA+PC=PE
问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG=.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是多少?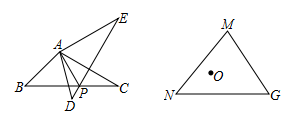
练习7、如图,在△ABC中,∠ACB=90°,AB=AC=1,P是△ABC内一点,求PA+PB+PC的最小值.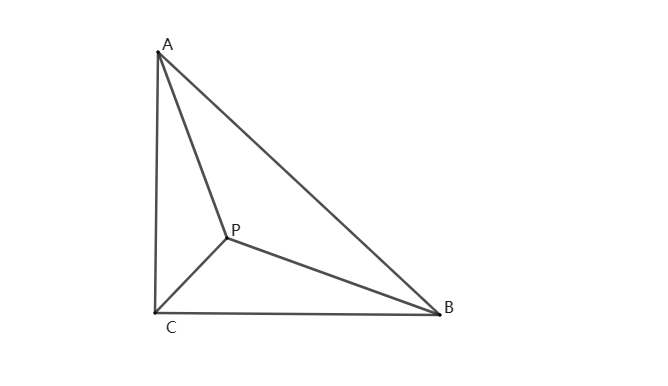
练习8、如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值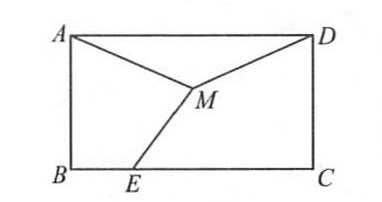
练习9、如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为\sqrt{3}+1时,求正方形的边长.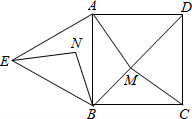
 在使用Docker时,经常会犯一个错,误以为latest镜像会自己更像到最小版本,其实这样理解是有问题的,latest就是一个标签,没有自动更新到最新版本的功能,本文就是对latest标签进行介绍。
在使用Docker时,经常会犯一个错,误以为latest镜像会自己更像到最小版本,其实这样理解是有问题的,latest就是一个标签,没有自动更新到最新版本的功能,本文就是对latest标签进行介绍。 人教版数学七年级下册第九章《不等式与不等式组》知识点:不等式、一元一次不等式、一元一次不等式的解法、一元一次不等式组及其解法等
人教版数学七年级下册第九章《不等式与不等式组》知识点:不等式、一元一次不等式、一元一次不等式的解法、一元一次不等式组及其解法等 初中数学:平面直角坐标系中四边形面积求法
初中数学:平面直角坐标系中四边形面积求法 人教版数学九年级上册第二十二章《二次函数》知识点:二次函数概念,二次函数y=ax^2,y=ax^2+k,y=a(x-h)^2,y=a(x-h)^2+k,y=ax^2+bx+c图象和性质
人教版数学九年级上册第二十二章《二次函数》知识点:二次函数概念,二次函数y=ax^2,y=ax^2+k,y=a(x-h)^2,y=a(x-h)^2+k,y=ax^2+bx+c图象和性质 人教版数学八年级下册第十六章《二次根式》知识点归纳,二次根式的概念,二次根式的性质,二次根式加减乘除,最简二次根式等
人教版数学八年级下册第十六章《二次根式》知识点归纳,二次根式的概念,二次根式的性质,二次根式加减乘除,最简二次根式等 快速生成表格
快速生成表格 打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration.
打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration. Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题
Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题 在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。
在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。 在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。
在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。