前面我们分析了二次函数存在性问题之直角三角形这类问题的解题方法，本文主要利用一线三垂直模型来求解，在利用该模型求解时，需要你已经掌握了相似三角形的性质。下面我们就来把前面的例题用一线三垂直模型来进行求解。

例、如图，在平面直角坐标系中，抛物线$y=a{x}^2+bx+c(a\ne 0)$与x轴相交于A，B两点，与y轴相交于点C，直线y=kx+n（k≠0）经过B，C两点，已知A（1，0），C（0，3），且BC=5．
（1）分别求直线BC和抛物线的解析式（关系式）；
（2）在抛物线的对称轴上是否存在点P，使得以B，C，P三点为顶点的三角形是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．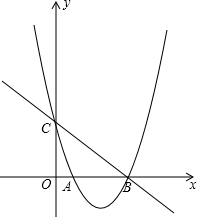

解：（1）∵ C(0，3)，即 OC=3，BC=5，

∴在Rt△BOC中，根据勾股定理得：OB=$\sqrt{B{C}^2-O{C}^2}$=4，即 B(4，0)，

把B与C坐标代入y=kx+n中，得：$\{\begin{array}{l}4k+n=0\\ n=3\end{array},$

解得：$k=-\frac{3}{4}，n=3$，

∴直线BC解析式为$y=-\frac{3}{4}x+3$；

由A（1，0），B（4，0），设抛物线解析式为$y=a(x-1)(x-4)$，

把C（0，3）代入得：a=$\frac{3}{4}$，

则抛物线解析式为$y=\frac{3}{4}{x}^2-\frac{15}{4}x+3$；

（2）存在，理由如下：

由（1）得，抛物线的对称轴为：$x=\frac{5}{2}$

∵ P点在抛物线的对称轴所在直线上，设P点坐标为($\frac{5}{2}$，m),

① 当∠CPB=90°时，如图，过点P作y轴的垂线，交y轴于点D，过B点作x轴的垂线，两垂线相交于点E，

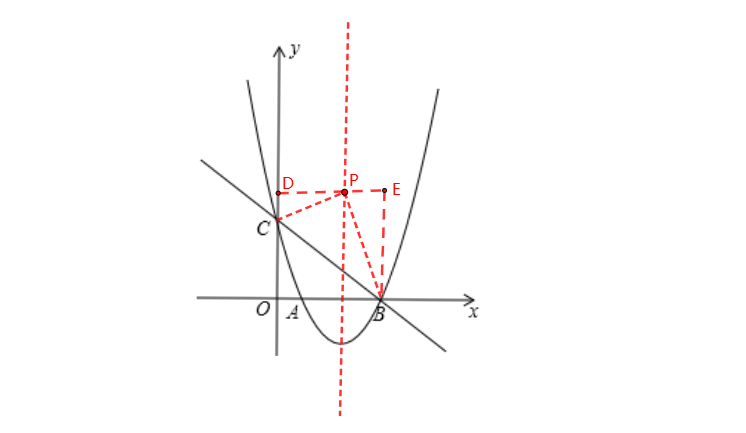
∵ A(1,0)、B(4,0)、C(0,3)

∴ D(0,m)，E(4,m)

则：DC=m-3，DP=$\frac{5}{2}$，PE=4-$\frac{5}{2}$=$\frac{3}{2}$，EB=m

∵ ∠CPB=90°，∠CDP=90°，∠PEB=90°

∴ ∠CPD+∠EPB=90°，∠CPD+∠PCD=90°

∴ ∠PCD=∠BPE

∴ △DCP∽△EPB

∴ DP:EB=DC:EP

∴ DP·EP=DC·EB

则：$\frac{5}{2}$×$\frac{3}{2}$=(m-3)·m

解得：m=$\frac{3}{2}+\sqrt{6}$或m=$\frac{3}{2}-\sqrt{6}$

则P点坐标为($\frac{5}{2},\frac{3}{2}+\sqrt{6}$)或($\frac{5}{2},\frac{3}{2}-\sqrt{6}$).

② 当∠PCB=90°时，如图，过点P作y轴的垂线，交y轴于点D，

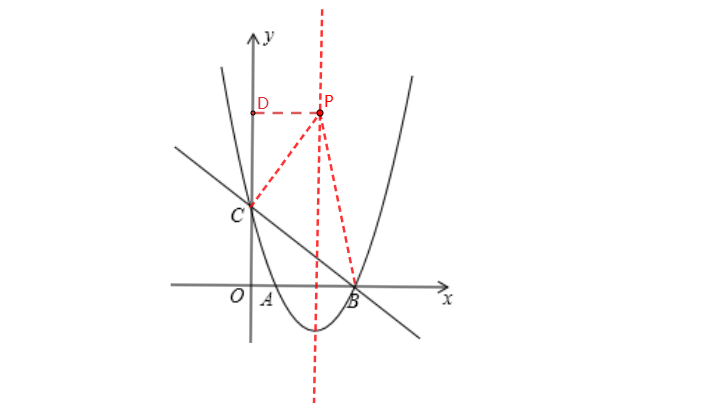
∵ A(1,0)、B(4,0)、C(0,3)

∴ D(0,m)

则：DC=m-3，DP=$\frac{5}{2}$，OC=3，OB=4

∵ ∠PCB=90°，∠CDP=90°，∠COB=90°

∴ ∠PCD+∠BCO=90°，∠BCO+∠OBC=90°

∴ ∠PCD=∠CBO

∴ △DCP∽△OBC

∴ DP:OC=DC:OB

∴ DP·OB=DC·OC

则：$\frac{5}{2}$×4=(m-3)×3

解得：m=$\frac{19}{3}$

则P点坐标为($\frac{5}{2},\frac{19}{3}$).

③ 当∠CBP=90°时，如图，过点B作x轴的垂线，过点C作y轴的垂线，交于点D，过点P作x轴平行线，交DB所在直线于点E，

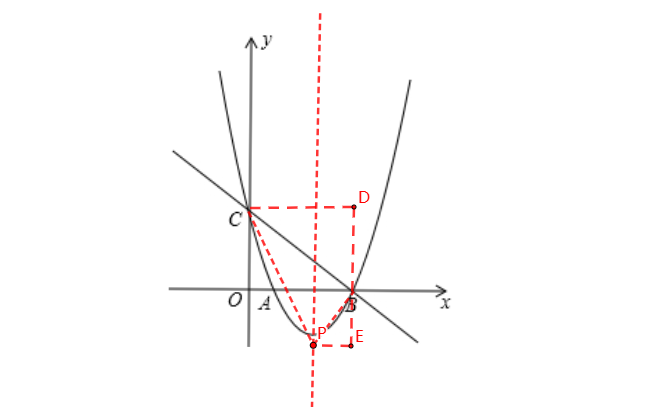
∵ A(1,0)、B(4,0)、C(0,3)

∴ D(4,3)，E(4,m)

则：DC=4，DB=3，BE=0-m=-m，PE=4-$\frac{5}{2}$=$\frac{3}{2}$

∵ ∠PBC=90°，∠CDB=90°，∠PEB=90°

∴ ∠CBD+∠PBE=90°，∠CBD+∠DCB=90°

∴ ∠DCB=∠PBE

∴ △DCB∽△EBP

∴ DC:EB=DB:EP

∴ DC·EP=DB·EB

则：4×$\frac{3}{2}$=3×(-m)

解得：m=-2

则P点坐标为($\frac{5}{2}$，-2 ).

综上所述，P点的坐标为：($\frac{5}{2}$，-2 )、($\frac{5}{2},\frac{3}{2}+\sqrt{6}$)、($\frac{5}{2},\frac{3}{2}-\sqrt{6}$)、($\frac{5}{2},\frac{19}{3}$).

练习、如图，抛物线$y=x^2-3x$与x轴相交于 O、A 两点，直线y=-x+3与y轴交于点B，与该抛物线交于A、D两点.在抛物线上是否存在点C，使△ABC为直角三角形?若存在，求出点C的坐标；若不存在，请说明理由.

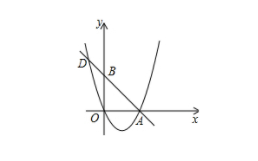
该练习题就留个给你们自己证明，一定要注意的C点在抛物线上而不是对称轴上，但是解题过程与上面相似，利用一线三垂直模型求解。

【答案】存在点 C，其坐标是(1,-2)或($2+\sqrt{7},5+\sqrt{7}$)或($2-\sqrt{7},5-\sqrt{7}$ )或(0,0)或$(\frac{3+\sqrt{17}}{2},2)$或$(\frac{3-\sqrt{17}}{2},2)$。